【Unity】ゲーム開発ではたまには高校数学も思い出すと便利です

タイトルを見て、「数学の話とか勘弁して！」なんて思ったりしたかもしれません。数学の教科書を買いなおしてセンターの過去問で数学IAとIIBで満点を取れるようになってください、なんて言わないので安心してください。

あとアイキャッチの数式を見て「いや物理やんけ！」と突っ込めたあなた、その調子でゲーム開発に数学や物理の知識を活かしして行けると思います。素晴らしい。

さて、このページのテーマはゲーム作りのときに思い出せると便利な数学の知識について。

ゲームを作っていると、高校数学の知識を使って機能を実装することもあります。例えば円の軌道を描くなら、三角関数の知識が使えます。X軸方向の位置は半径かけるcosθ、Y軸方向の位置は半径かけるsinθを使って表すことができます。

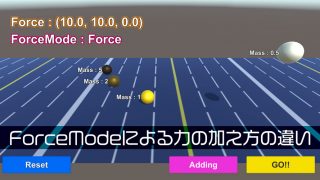
また、Rigidbodyで力を加えるときにも力の分解が使えます。これは若干物理っぽいですが、物理でも数学を使っていることを考えれば一応今回のテーマの範囲でいいかな。例えばこんな感じ。力を加える方向は地面から何度の方向で、水平方向の力はこれくらい、垂直方向の力はこれくらい、という感じで分解しています。

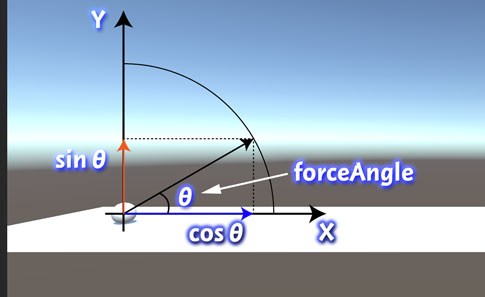
このように、Unityによる物理的な演算の他にも、スクリプトから数学的な計算を行うことはよくあります。オブジェクトの位置を計算するためにスクリプト内でMathf.Sine()などを使えると実装できる機能の幅も広がりますね。

例えばベクトルの計算

よく使っているVector2とかVector3などに用意されているメソッドでは、ベクトルの計算を使ったものもあるのでこの辺りも高校数学の知識を思い出すと便利です。

例えば、主人公の位置から一番近い敵キャラを割り出す際にベクトルの大きさ(magnitude)の考え方を使って計算することができます。3Dでも2Dでも、ベクトルを使えば敵キャラまでの距離を割り出すことができますから、magnitudeが一番小さい敵キャラを特定して、オートターゲットのように攻撃対象として設定することもできます。

あるいは、あるオブジェクトから別のオブジェクトへの向きを計算したいときには、ベクトルの引き算をした後に規格化(normalized)を使って単位ベクトルを算出すると便利です。方向だけ割り出して、そちらの方向にどれくらい近く、みたいな処理も実現できます。

ベクトルに関しては物理のときに嫌と言うほどいじった人もいるかもしれません。「もうベクトルの合成や分解はしたくないです……」という場合でもちょっとだけ頑張ってみると「意外と大したことないな？」と自信がつくと思います。

エフェクトでも便利

スクリプト以外でも、例えばVisual Effect Graphやパーティクルの起動を計算する時にも高校数学の知識があれば円の軌道を簡単に描くことができます。

Visual Effect Graphに関しては『Unity デザイナーズ・バイブル』の中で寄稿したのですが、この中でも簡単に円の軌道を使うことによって中心位置の周囲を飛び回るような水のリングを表現しています。

高校数学の式をそのまま使ってしまうことで、Visual Effect Graphで作るノードの数も減らせます。ノードのカテゴリとして数学的な計算を行うノードもたくさん用意されているので、使える知識があればあるほど楽にエフェクトを作成することができるようになります。

ノードとして高校数学のパーツを見るとちょっと「うっ！」となるかもしれませんが、実際に使ってみると「なんとなくこれやったな？」と思い出すことができると思います。

三角関数をいじれると強い

個人的にゲームを作るという意味でおすすめしたいのは三角関数の分野です。サイン、コサイン、タンジェント。

周期的な運動や、円形の描画など、ちょっといじるだけでもたくさんのバリエーションを生み出すことができます。そのため、ここだけに集中してみるのもいいかもしれません。

ゲーム作りの場合は、プログラムを動かすだけではなく、画面に描画される動きも重要ですからね。

流石にarcsinとかarccosまで勉強しよう！　とまでは言わないので、調べた公式の意味が分かる程度でも大丈夫です。

より頑張るなら論理や集合も

ゲーム作りのプログラミングというより、コンピュータサイエンスまで勉強したい場合は論理や集合についても調べておきましょう。

真と偽……とくればTrue/Falseのbool値でお馴染みですが、if文の条件として使っていますよね。この辺りの足元を固めておくことで、条件式を作る場合も漏れなく重複なく作ることができます。

ベン図とか覚えていますか？　条件Aが示す範囲と、条件Bが示す範囲があって、重なり合っている部分を取るのか(AND条件)、それともどちらかに含まれていればいいのか(OR条件)、といった考え方も実は高校の時にやっているんですよね。

あとは条件をひっくり返したらどうなるかみたいなのもやったと思います(ドモルガンの法則)

この辺りもいい感じの条件式を作る時には思い出しておくと便利です。テストの時には書いた条件式そのものが正しいことを確かめる他に、そもそもこの条件式で想定されるケースを網羅しているのか、みたいな観点も必要になるので、ぜひマスターしたいところ。

コンピュータサイエンスになると「回路」の考え方とかが出てきてちょっと複雑になりますが、その基礎となる論理や集合の部分を固めておくと良いと思います。私は新卒で入った会社の研修で叩き込まれたので、なんだかんだ今でも役に立ってます。ありがたい。

解説サイトは結構あるよ

「数学とかめっちゃ苦手です！」という場合は、ググると分かりやすく解説しているブログも結構多いので、簡単に眺めてみると良いかもしれません。

内容を細かく見るのもいいですし、単元の名前を見て「そういえばこういうのもあったなー」と思い出すだけでもあなたの記憶が活性化すると思います。可能なら、数式がそのまま載っていて、かつ解説が平易な言葉で書かれているサイトを探すと良いでしょう。

教科書のような情報を参照するなら、普通に教科書を見た方が安心できますからね。自分の理解を助けるための解説に意味があるのです。

ゲームを作るなら数学ができるに越したことはないので、外出がしづらい今の時期に数学の知識をおさらいしておくと良いかもしれません。

とはいえ、数学ができなければゲームを作っちゃいけないなんてことは全然ないので、レベルアップしたいなーという時に高校数学をおさらいしてみよう、ぐらいの温度感です。

まとめ

ゲーム作りでは数学の知識があると便利な場面が多いので、もしレベルアップしたいと思ったら高校数学レベルから復習しておくと役に立ちます。

数値的な計算に加えて、エフェクトに関しても生かせる場面があるため、やって損はありません。