【Unity】なんとカーブと乱数を使って確率を決められるらしいぞ!
乱数で遊んでいると日が暮れちゃうくらい楽しいですね。最近は乱数と確率で遊んでばっかな気がします。
前回は重み付きの抽選をテーマに、ゲームで敵を倒した時に発生するアイテムドロップのサンプルを実装してみました。
Unityのマニュアルでも『異なる発生確率を持ったアイテムを選択する』としてサンプルコードがあったので、それをアレンジした形です。個別の事象に対してそれぞれ確率が設定されている場合に有効な方法でした。
今回扱いたいのは、同じくUnityのマニュアルが出発点の『連続確率変数への重み付け』です。宝箱を開けたら、10Gから100Gの間でランダムにお金を入手させたい、なんて時に使うケースです。
10Gから100Gの全ての金額に発生確率を設定するのは超絶めんどくさいので、Unityの機能であるAnimationCurveを使って簡単に重み付きの値を引っ張るテクニックです。
環境
macOS 10.13 High Sierra
Unity2018.1.0f2
連続確率変数とは
漢字を見るとごついですね。
10, 10.1, 10.2, … , 99.9, 100といったように連続した値の中からどれか1つをピックアップするとき、この連続した値を連続確率変数と呼びます。
冒頭で挙げた例のように宝箱からお金を入手する場合は10, 11, 12, …とint型に変換するのが望ましいですが、TransformのPositionとかであればfloat型で連続的な値をとった方がいいかもしれません。
これに対して、サイコロの目とか敵のドロップアイテムなど、それぞれの結果が離散的であるものは離散確率変数です。サイコロで『2.83』とか『3.46』の目が出るとかないですもんね。『1』『2』『3』といったように飛び飛びの値を取るので離散的です。
前回までの乱数は離散確率変数でしたが、今回は連続確率変数に触れます。乱数は確率と切っても切れない縁があるためか、確率論の話に入ってしまうこともあります。
カーブを使おう
連続する変数というと、中学校の頃に習った二次関数を思い出します。
$$f(x)=a{x}^2+b{x}+c$$
この中ではXが連続的な値を取りうる変数でしたが、連続確率変数でも似たような感じです。
特に今回はカーブを使って値を取得するので、グラフから値を読み取る点も似ているかもしれません。
UnityではAnimationCurveという機能があり、引数でX軸の値を渡すと、カーブの形に応じてY軸の値を返してくれます。
例えば以下のようなAnimationCurveがあったとします。
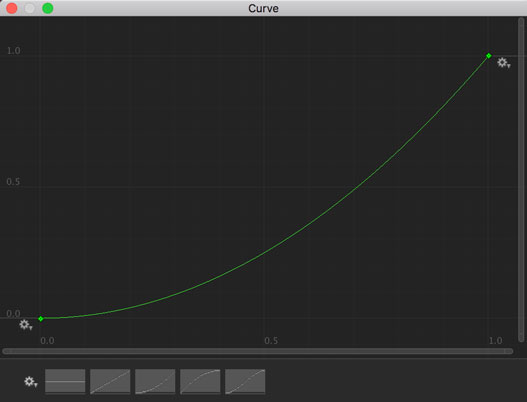
このカーブに対して上記のスクリプトから値を与えて計算すると以下のように値が返ってきます。メンバ変数としてAnimationCurveを指定しておけば1行で値を取得できる点が超絶便利。
| 入力値 | 戻り値 |
| 0.25 | 0.0625 |
| 0.5 | 0.25 |
| 0.75 | 0.5625 |
綺麗に\(y={x}^2\)の形になっていました。
この時の入力値を乱数で指定することにより、戻り値もまたランダムに返ってくることになります。さらに、カーブによる補正があることから、重み付けがなされた状態で値を得ることができます。
例えばRandom.valueで入力値を指定すると、0から1までが指定されることになります。上のカーブであれば、0から0.5までの入力値では、戻ってくる値は0から0.25の範囲。つまり、50%の確率で低い値が返ってくることに。
カーブが緩やかだとその範囲の値を取りやすく、逆にカーブが急になるとその範囲の値はなかなか出てこないことになります。カーブが急ということはX軸の区間が短いということ。X軸の区間が短いと、乱数がその区間の値を取る確率が低いということになります。
Unityのマニュアルでも書かれていますが、このカーブそのものは確率分布曲線じゃないので注意。\(x=1\)の時、Y軸の値が1であることから、Xが大きいほど確率が高い、なんて誤解しちゃうこともあるかも。
マニュアルでは、
確立分布曲線ではなく、もっと逆累積分布曲線のようであると気付いてください。
と一瞬戸惑う日本語がありますが、原文ではmore likeとあったので、『確率分布曲線というよりむしろ逆累積分布曲線に近いです』という意味だと思います。
逆累積分布曲線は……うん、扱わないようにしよう。迂闊に深淵を覗き込むと、深淵に覗き込まれますからね。
ここでは、カーブに応じてどんな確率分布曲線が描かれるのかを確かめてみましょうか。
感謝の10000回ループ
スクリプトを使って、10000回ほど乱数を生成し、それを使ってカーブから値を取得します。
取得した値はCSVファイルに書き出して、ExcelなりNumbersで集計し、取得した値と発生確率でグラフ化したいと思います。
データを確認するためのスクリプトはこちら。
AnimationCurveはEvaluateメソッドを使うと、引数に該当するカーブの値を返します。
それを10000回繰り返し、結果の値の分布を確認します。
なお、分布を計算しやすくするため、MathfのRoundToIntを使ってfloatの値を100倍した後intに丸めています。これに伴い0と100の値がおそらく理論値より低くなってしまいますが、確率分布曲線の概形だけ見られればいいので今回は目を瞑りたいと思います。
例えば宝箱から入手する金貨などのようにint型に変換する必要がある場合は、カーブからfloatで値を取得してRoundToIntによって丸め込むことが考えられます。この時も実験と同様に、最小値と最大値を取りうる確率が低くなる可能性があるので注意です。
分布を確認するための区間として0から100までの101個の区間を考えており、AnimationCurveから取得した値がこれらの区間に入った数をカウントし、SortedDictionaryに記録しています。KeyVakuePairをforeachで取り出す際、順番がソートされているとグラフ化するのに便利だったので、SortedDictionaryを使っています。
10000回の値取得が終わったらCSVファイルに出力しています。ファイルへの出力を行うため、System.IOの名前空間を追加しているのでお忘れなく。
実行結果
上記のスクリプトを任意のゲームオブジェクトにアタッチしてゲームを実行した結果がこちら。
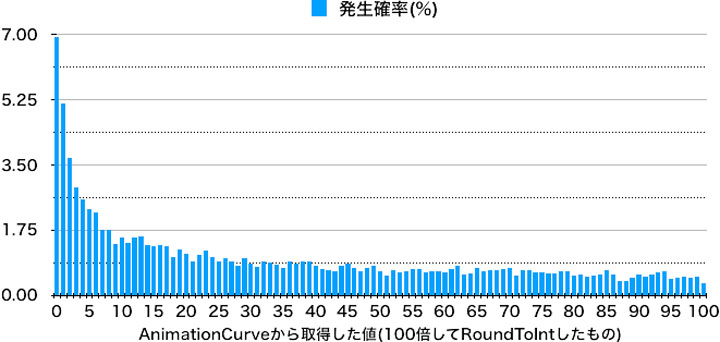
AnimationCurveで定義されたカーブにおいて、緩やかだった部分は発生確率が大きく、急な部分は発生確率が低くなっています。
二次関数\(y={x}^2\)でも、xの値が低ければなかなか値が増えていかないので、低い値になる可能性が高くなるのと似ています。
結果の値が0から25となったケースをカウントすると、50.43%とAnimationCurveのX軸と連動していることがわかります。
この曲線だと、低い値が出やすいように重み付けがされている、と言えます。
まとめ
連続的な確率変数の場合は、AnimationCurveを使って重み付けをすると非常に便利です。
使える場面も結構多く、ランダムな体力回復だったり、宝箱からのランダムな枚数の金貨入手、アニメーションでTransformの位置をランダムにセットするなど、一度触っておくと応用が効きます。
カーブを使うとなると少し取っ付きにくいかもしれませんが、スクリプトを動かして動きを確認するとそんなに難しく感じないかも。
ゲーム開発の攻略チャートを作りました!
-
前の記事

【Unity】UnityのRandomを使って重み付き抽選を実装するサンプル 2018.06.23
-
次の記事

【Unity】乱数を使ってAnimationCurveに応じた確率分布曲線を描く 2018.06.25























コメントを書く