【Unity】乱数を使ってサイコロの1から6が全部出るまで走る逆鱗マラソン

最近は乱数にハマっていて、ゲーム内で使用する乱数について色々と実験をしています。
UnityではRandomクラスを使って簡単に乱数を取得することができます。これを使って、敵キャラがアイテムをドロップする確率の目安を考えています。
前回は、ある1体の敵キャラが6種類のアイテムをドロップするとき、全てのアイテムのドロップ率が1/6でサイコロと同じだった場合に、少ない試行回数でアイテムを集め終わるユーザーがどれだけいるのかをシミュレーションしてみました。
この6種類のアイテムを集めると最強の武器を作れる設定で、モンハンの武器とか世界樹の迷宮に出てくる真龍の剣みたいなイメージです。通称逆鱗マラソン。
結果として、試行回数が10回だと、10000人のユーザーのうち、全部アイテムを集めたユーザーは2700人程度で、2, 3種類しかアイテムを集められないユーザーが200人ほどいました。
試行回数が少ないと確率論的には全然アイテムが手に入らないのも想定内ですが、ユーザーの立場だと乱数の「偏り」に感じられる気がします。特に上記の200人は「偏ってる!」と声高に叫ぶことでしょう。
さて今回は試行回数の上限を取っ払い、各ユーザーが武器を作るまでにかかった討伐回数をカウントします。同じく10000人が武器を作るまで逆鱗マラソンを頑張ったとして、その平均値、最小値、最大値を求めます。期待値は14.7回なので、その通りになるかも確認します。
揃うまで頑張る逆鱗マラソン
各ユーザーごとに素材が6種類揃うまで何度でもボスを倒し続けるケースを考えます。期待値、最小値、最大値は以下の通り。期待値は、集計後に各ユーザーごとのボス討伐回数を平均したものと比較します。
| 項目 | 理論値 |
| 期待値 | 14.7回 |
| 最小値 | 6回 |
| 最大値 | ∞回 |
期待値の計算はクーポンコレクター問題における期待値の計算式をそのまま使えます。
n種類の要素が揃う時の期待値Eは、
$$E=n\cdot\left(\frac{1}{1}+\frac{1}{2}+\ldots+\frac{1}{n}\right)$$
で求められるので、n=6のとき、
$$E=6\cdot\left(\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}\right)=14.7$$
となります。期待値が10回を超えているので、前回やった10回の討伐ではそもそも揃う人の方が少ないんです。でも1/6って聞くと10回でいけちゃいそうな気がする不思議。
最小値はサイコロの目の数である6回。激運ですね。
最大値は理論上∞回になります。確率が0でなければ起こる可能性はあるので、無限回の試行が必要になることも。
これらの理論値と、実際にスクリプトで乱数を取得した結果を比較し、UnityのRandomクラスが確率論の観点からいい感じだということを確かめます。
確認用のスクリプト
上記の逆鱗マラソンを再現したスクリプトがこちら。いやもうほんとすんません、200行ほどと、すっごい長くなっちゃいました。
やっているのは、ボスがドロップする素材6種類を全部集めるまで討伐し続けるのを10000人分繰り返すこと。
RollADice()の中ではUnityのRandom.Rangeを使って、サイコロの目に合わせた範囲で乱数を取得しています。
その乱数が1から6まで揃うまでループし、全部揃ったところでRecordStatメソッドの中でメンバ変数に値を記録しています。
最小値、最大値については現在保存されている値との比較を行い、平均値算出用のカウントについてはそのまま試行回数を加算しています。
10000人分の処理が終わったら、カウントから平均値を割り出し、CSVファイルに出力しています。
結果はこちら
上記のスクリプトを適当なゲームオブジェクトにアタッチしてゲームを実行すると、OutputDiceResultsWithAllTypeの中で指定したパスにCSVファイルが出力されます。
そのCSVファイルに記録された平均値、最小値、最大値は以下の通りでした。
| 項目 | 理論値 | 実行結果 |
| 期待値(平均値) | 14.7回 | 14.8323回 |
| 最小値 | 6回 | 6回 |
| 最大値 | ∞回 | 80回 |
実行結果の平均値は概ね期待値通りでした。前回の結果もそうでしたが、UnityのRandomクラスの乱数は確率論に沿っている気がします。
最小値は理論値通りの6回。レアケースではあるものの、引く人は引きます。裏山。
最大値が無限回まで行かなくてよかったーと言いたいところですが、80回も中々きつい数字です。ドロップ率16.67%で80回までハマるとか泣いてもいいよもう。ドロ率3%とかだったらどうなっていたことやら……。
なお、10000人の実行結果の分布は以下の通りです。
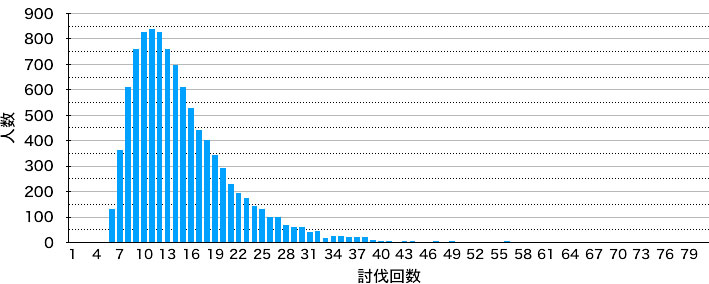
11回目で達成した人が一番多かったようです。30回目の時点で約9700人が達成していたので、残りの300人には強力な物欲センサーが働いていたのかも。
結果から言えること
ドロップ率16.67%という高確率ですら苦行になりうることが分かりました。開発者の立場だと、いっぱい遊んで欲しいからドロップ率を絞る、なんてことをしてしまいがちですが、一部のユーザーにとっては苦痛になってしまう可能性があります。
冒頭でモンハンや世界樹の例を挙げましたが、モンハンでは部位破壊による報酬枠の追加やクエストに応じた確定(あるいは高確率)の報酬、世界樹では使ったターンに敵を倒すと確実に戦利品をドロップするアイテム『解剖用水溶液』の存在など、通常の確率ドロップだけではアイテムを入手できないユーザーへの救済措置があります。
こうした救済措置をゲームに入れておくとユーザーのストレスが減ります。確率ドロップでは少数のユーザーが確率の悪魔(物欲センサー)に囚われてしまいますもんね。
今回はサイコロと同じ確率で計算してみましたが、重み付きの抽選でも確認してみようかな。Unityの『ランダムなゲームプレイ要素の追加』にもサンプルコードがあったので、次の記事では重み付きの抽選をやってみようと思います。
おまけ
乱数を使って、当たりを引くまで終わらない脱出ゲームを作りました。脱出に必要なのはゴールを引き当てる運だけです。
ブラウザで遊べるのでこちらも是非。
ゲーム開発の攻略チャートを作りました!
-
前の記事

【Unity】少ない試行回数で乱数が偏っているように感じる件を調査 2018.06.22
-
次の記事

【Unity】UnityのRandomを使って重み付き抽選を実装するサンプル 2018.06.23

























コメントを書く