【Unity】乱数を使ってAnimationCurveに応じた確率分布曲線を描く

最近は乱数にはまっています。前回は乱数とAnimationCurveを使って、連続的な確率変数に重み付けをして値を取り出す方法を試してみました。

エクスプラボ

 

1 Pocket

【Unity】なんとカーブと乱数を使って確率を決められるらしいぞ!

https://ekulabo.com/random-in-curve

AnimationCurveを使って、連続的な確率変数に重み付けをします。Unityのマニュアルを出発点に、10000回ランダムな値を取得し、その確率分布曲線を出してみます。視覚的に重み付けができるのが一番のメリットかも。

上の記事ではひとつのカーブを例に確率分布曲線を描いてみたのですが、プリセットは全部で5種類あるため、それらについて確率分布曲線を描いてみたいと思います。

AnimationCurveの見た目と確率分布曲線は異なるので、実際に値を取り出してみて大まかな形を掴むといいかも。

環境

macOS 10.13 High Sierra

Unity2018.1.0f2

連続確率変数について

どのような結果が得られるかが確率で決まっている変数を確率変数と呼びますが、この確率変数には2種類のものがあります。

ひとつは離散確率変数で、サイコロの目のように『1』『2』『3』といった形で飛び飛びの値を取るものです。サイコロの目は『2.83』とか『3.46』といった目は出ないので、値が連続していないんです。

もう一方は連続確率変数で、数直線上の値のように1.0から10.0までの間のいずれかの値を取りうるものです。サイコロと違って『2』『3』『4』だけではなく、その間にある『2.83』とか『3.46』も取ります。このように連続している値が変数となっているので連続確率変数です。

今回使うのは連続確率変数で、AnimationCurveを使って重み付けをすることができます。

エクスプラボ

 

1 Pocket

【Unity】なんとカーブと乱数を使って確率を決められるらしいぞ!

https://ekulabo.com/random-in-curve

AnimationCurveを使って、連続的な確率変数に重み付けをします。Unityのマニュアルを出発点に、10000回ランダムな値を取得し、その確率分布曲線を出してみます。視覚的に重み付けができるのが一番のメリットかも。

その詳細については上の記事で扱っているので、こちらもご覧あれ。

実験方法

UnityのRandomクラスを使って乱数を発生させ、AnimationCurveによって重み付けがなされた値を取得します。

得られる値はfloatなのでその値を100倍し、RoundToIntによって整数にして数をカウントします。

floatで集計すると確率を出すのがものっそいしんどいので一番近い整数の値を基準として、その数字が何回出たかを集計する形とします。

デメリットとして0と100の発生確率だけ下がってしまいますが、ざっくりと分布が見られればOKとしています。

以下の画像は前回の実験結果です。このようなイメージでカーブの形に応じた確率の分布を出してみたいと思います。

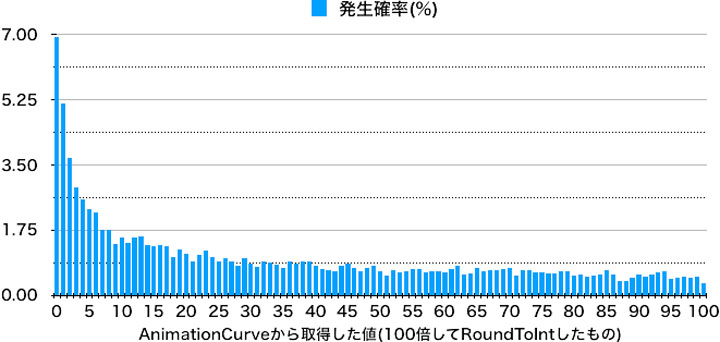
……確率分布曲線と言いながら棒グラフですが、何とか心の目で曲線を読み取ってください。

スクリプト

上記の実験方法を盛り込んだスクリプトはこちら。

curve.EvaluateにX軸の値を渡すと、カーブの形に応じて値を返してくれます。

その値をExcelやNumbersで集計したかったので、CSVに結果を出力する処理も。

なお、カーブの形やファイル名はInspectorウィンドウから変えられるようにしています。

これを任意のゲームオブジェクトにアタッチし、ゲームを実行することでカーブの形に応じた確率分布曲線を出してみます。

実験結果

定数

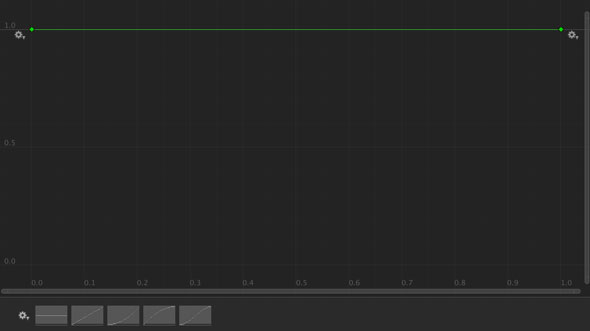
上記のカーブを使って確率分布曲線を出すと以下のようになります。

どんな値をカーブに渡しても1しか返しません。よって100%の確率で固定値です。固定値は裏切らない。

一次関数

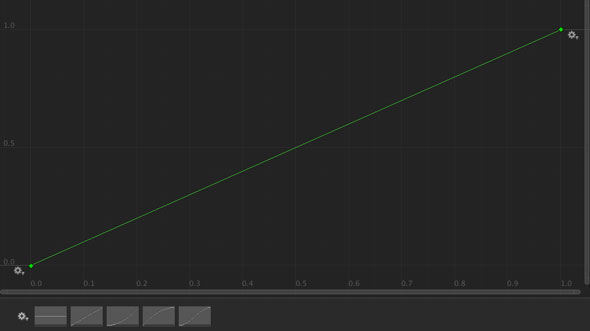
上記のカーブから出した確率分布曲線は以下のもの。

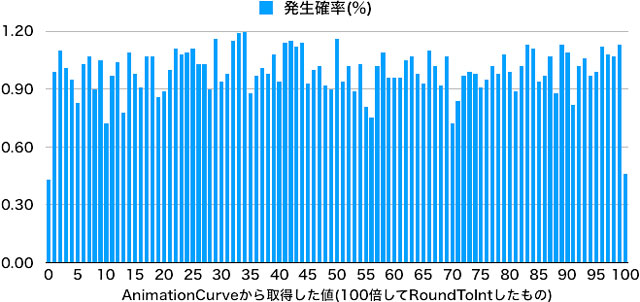
全体的に1%前後になっています。顕著な揺らぎは見られません(主観)

なお、RoundToIntしている関係で、0と100は半分程度の値となっています。RoundToIntは一番近い整数にするので、0fから0.5fまでは0に、0.5より大きく1.5より小さい場合は1に……という感じなので、0だけ発生確率が半分になっちゃうんです。

例えば宝箱からランダムな枚数の金貨を手に入れる場合など、AnimationCurveを使って取得した値を最終的に整数型にするケースでは注意が必要です。

二次関数

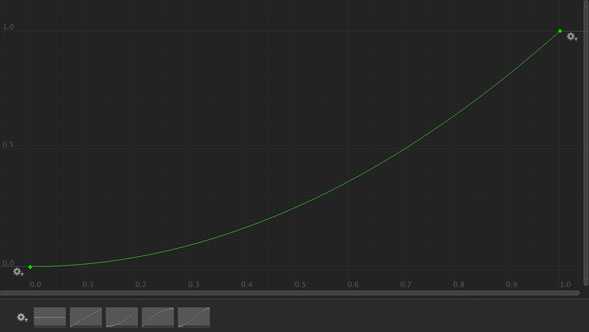
ここから重み付けが始まります。緩やかに上昇する部分は発生確率が高く、急に上昇している部分は発生確率が低くなります。

例えば上のカーブだと、X軸が0から0.5までの間は緩やかに上昇しています。X軸の値が0.5の時の結果は0.25となることから、最終結果が0から0.25までの値となる確率が50%なので、緩やかだと発生しやすいことになります。

今回はプリセットを使っていますが、重み付けのために自分でカーブを描くときには緩急をつける必要があります。

このカーブを使って確率分布曲線を出すとこうなります。

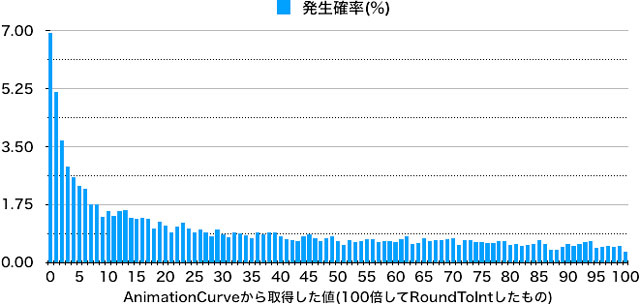
カーブの緩い部分である小さい値が出やすく、カーブが急になる大きな値は出にくくなっていました。

二次関数(逆向き)

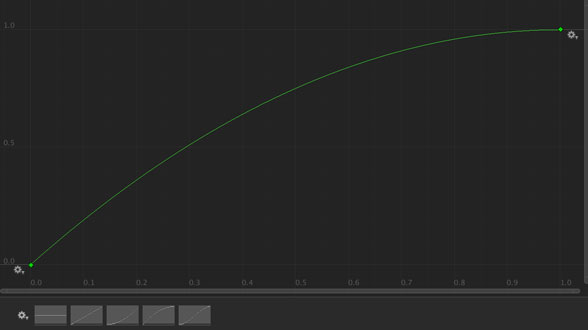
ひとつ上のカーブを上下逆にしたようなケース。値が大きくなると増えかたが緩やかになるので、大きな値が出やすいはず。

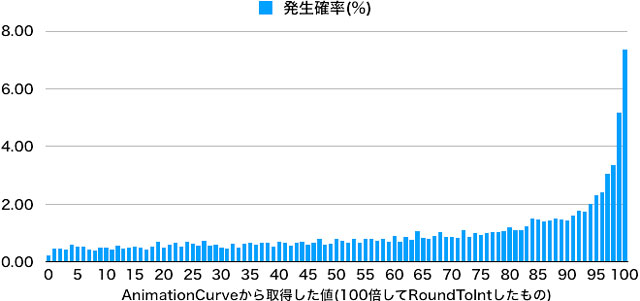
よしよし、いい感じいい感じ。

上のカーブとは綺麗に左右逆になっています。

イーズイン・イーズアウト

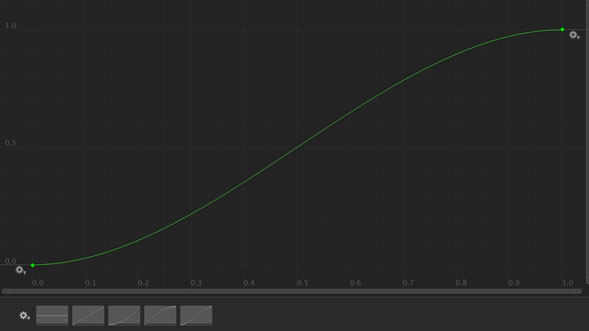
呼び方が正しいかは分からないのですが、最初が緩やかに始まって、中程は直線的に増え、最後にまた緩やかになるカーブです。

緩やかポイントが最初と最後なので、そこで確率が大きくなるはず。

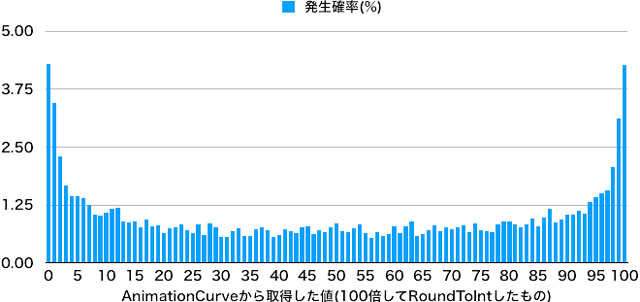
いい感じです。

緩やかポイントさえ見抜けば、確率が大きくなる場所にあたりをつけることができそう。

オリジナルカーブ

自分でカーブを作ってみたらどうなるかな。

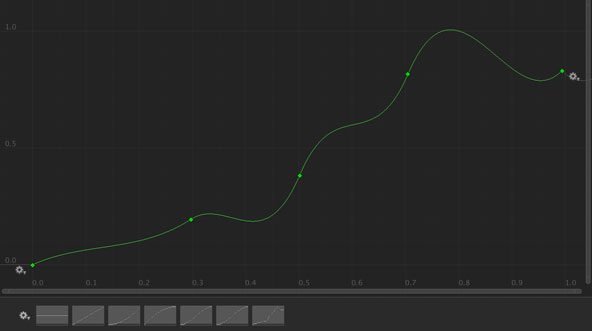
ぐっちゃぐちゃカーブのなので、どこが確率高くなるのやら……。

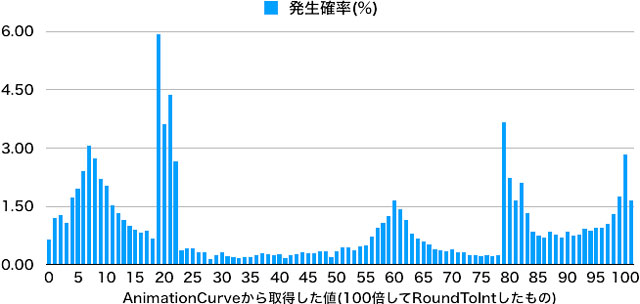
うーん……。低い値の方が比較的出やすいかな。折り返しがある辺りは流石に出やすくなってますね。

こんな感じでオリジナルのカーブでも乱数を使うことができます。20と70を出やすくしたい、なんてときにはその周辺でカーブを上下させると良さそう。

まとめ

AnimationCurveごとの確率分布曲線を描いてみる実験でした。

カーブからどの値が出やすいかを見極めるには、緩やかポイントを見つけるのがコツです。

小さい値が出やすい、大きい値が出やすいなど、シンプルな重み付けであればプリセットでも十分使えるので、この辺りから使ってみるといいかも。