【Unity】MathfのSinとCosを使って円形の軌道を描くサンプル【C#】

Unityには数学的計算を行うのに便利なクラスとして「Mathf」が用意されています。名前からして数学が得意そうですね。

このクラスは大体の数学的計算を行うメソッドが用意されているので、なにかしら数学っぽい計算をしたいときにはMathfクラスを使うと便利です。

このページではとてもシンプルな例としてsin(サイン)とcos(コサイン)を使って円形の軌道を描くサンプルを紹介します。

MathfのSinとCosを使って円形の軌道を描くサンプル

Mathfにはsinとcosの値を計算してくれるメソッドがあるので、これを使えば円形の軌道を割と簡単に描くことができます。高校数学の知識なのでおそらくあなたも一度は触れているはずです。物理を履修していれば呼吸をするかのように使っていたと思います。

覚えていなくても「単位円」でググれば簡単に方程式が出てくるので、そのまま使えばOKです。プログラミングのいいところは答えを調べながらモノを作れるところですね。

さて、円周上の位置を表す場合には、以下のようにx方向とy方向に分解して座標を表すと簡単です。

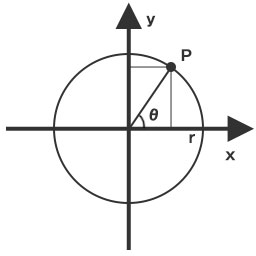
例えば上の画像のように円周上の点Pの座標を表す場合は、原点から点Pまでの直線とx軸との角度θを使って以下のように表せます。(rは円の半径)

\(P(r \cdot \cos \theta,\ r \cdot \sin \theta)\)

x方向の成分が\(\cos \theta\)でy方向の成分が\(\sin \theta\)なのは以下の図を見ると分かりやすいかもしれません。

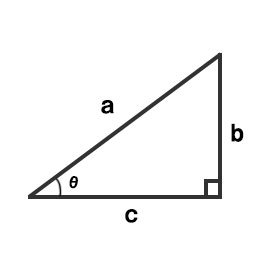
三角比の定義では以下のように表されます。

\(\cos \theta = \frac{c}{a}\)

\(\sin \theta = \frac{b}{a}\)

例えばx成分に相当するのはcの辺ですから、\(\cos \theta\)の式を変形するとcの値を求められます。ここではaに相当するのは半径のrなので、上の方で示した座標のように表されます。

この座標の表し方を使うと、\(\theta\)が変わったとしても計算できそうです。周期的に角度が変わるようにすれば、円周上をオブジェクトが移動する様子を作成することができます。

平面上を動く球の作成

sinとcosを使って円周上を移動するオブジェクトを作成します。

まずはシーンを作成し、以下のようにPlaneオブジェクトの上にSphereオブジェクトを作成します。位置やスケールはいい感じに配置するとグッド。

Sphereオブジェクトが平面上を動くようにしたいので、Sphereオブジェクトにスクリプトをアタッチして位置を動かしてみます。

スクリプトの作成

スクリプトファイルを作成してこれを編集していきましょう。名前は任意でOKです。下の画像では『SphereMover』にしました。

作成したスクリプトでは以下のように編集します。

フィールドとして作成しているradiusは円の半径です。ここでもう一度懐かしの円に登場してもらうと、円の半径rに相当します。今回のサンプルではシーンの原点の周りをぐるぐるするようにしています。

initPosはゲーム開始時のSphereオブジェクトの位置です。この内、高さの値であるtransform.positionのyは一定にしておきたいのでフィールドに保持しておくようにしてます。このフィールドに対してはStart()の中で値をセットします。

Update()ではオブジェクトの位置を計算するメソッドを呼んでいて、上の図の\(\theta\)のように角度をphaseのローカル変数に代入しています。このサンプルでは1秒で1周するようにしていて、ゲーム開始からの経過時間に\(2\pi\)をかけています。Mathfでは\(\pi\)の値も定義されているのでそのまま使えます。

現在の位置を計算する時には、

\(P(r \cdot \cos \theta,\ r \cdot \sin \theta)\)

を使って計算しています。Mathf.CosやMathf.Sinを使ってそのまま計算できるのが嬉しい点です。引数に角度を渡すようになっているので、上で計算したphaseを渡しています。

あとはいつものようにVector3で位置を表現し、それをtransform.positionに代入しています。

動作確認

スクリプトを保存してSphereオブジェクトにアタッチした上でゲームを実行すると、以下のようにSphereが円周上でぐるぐる回るようになります。

回転速度のフィールドを用意してphaseの計算時に使うことで、Sphereオブジェクトをさらに速く回転させたり、逆にゆっくり回転させたりできます。

公式をそのまま使うだけでもオブジェクトを動かせちゃうので、高校数学の教科書を眺めているとお宝の山のように感じるかもしれません。

その他の応用例

キャラクターを動かすために使うというよりは、ステージ内の雰囲気作りのオブジェクトで使うのがいいかもしれません。スクリプト内から直接transformをいじっているので、Rigidbodyなどとの兼ね合いを考えると、衝突に関連するオブジェクトでは使わないのが安心です。

また他の例としては、エフェクトにも応用できます。Mathfクラスをそのままスクリプトで使うというよりは、この考え方を応用する形になりますが、Visual Effect Graphでエフェクトを作る際に円の動きを作るために使うとこれがまた便利なんですよね。

Cosのノードを使ったりSinのノードを使ったりすることでパーティクルの出現位置を変えることができるので、円の動きを表現したい時には三角関数を使うと非常に便利です。

まとめ

1年も終わるし、円満に終わった感じで円に関することを書いてみよう、という軽いノリの記事でした。

Mathfクラスはぱっと見「数学とか辛いよ……」と敬遠してしまうこともあるかもしれませんが、実は高校数学の公式をそのまま使うだけでもいい感じにオブジェクトを動かせたりします。なので軽いノリでスクリプトリファレンスを眺めてみるといいかもしれません。

過去に学んだことを生かすという意味でも年末にふさわしい記事でしたね(自画自賛)