【Unity】floatの計算で誤差が出る理由をビット列で見てみよう【C#】

「floatの計算って誤差が出るんだよなぁ」

と日々悩み抜いて誤差の沼に足を踏み入れたあなたに読んでいただくためにこの記事をまとめました。

floatやdoubleなどの浮動小数点数を使った計算は誤差がつきもので、以下のようにfloatの足し算をした時にその値を比較すると、思わぬ結果になったりします。

この例では0.1を10回足したら1.0になるはず……と思っていると、実はif文の条件式がTrueにならないという罠があります。この辺りは人間の感覚とコンピュータでズレのある部分ですね。

floatなどの浮動小数点数だと誤差が目立ちがちな理由を記事の中で解説していきます。またUnityでfloatの値を比較する場合にどうすれば良いかについても紹介します。

浮動小数点数には誤差がつきもの

ただ数えていけば良い整数と違って、小数を表現するのは至難の技です。コンピュータではひとつの変数に割り当てるビット数を決めて値を認識しているので、どうしてもそのビット数に収まる範囲でしか値を表現できません。

「コンピュータちゃんにも苦手な事があるのね。うふふ」

と思ったあなた。まさにあなたにやってもらいたいのが以下の課題。

「数字を使って円周率を正確に記述してください。」

……無理ですよね、こんなん。あ、本当にやらなくて大丈夫ですよ。

人間でも表現しきれない小数があるんです。例えば円周率であればπという記号で表現することもありますし、3.14として計算するケースもあります。3で計算することもあるかもしれません。

私たちは円周率のような無理数であれば、表現できる範囲で値を使っています。3.14の後に続く1592..の部分は使わずに近似的に値を計算しているんですね。この時、実際の値と計算による値が異なるので誤差が生まれています。例えばこの場合は1592..の1の部分を四捨五入して0として計算しています。四捨五入による丸めで誤差が生まれていることから、丸め誤差と呼ばれます。

コンピュータでも同じように、表現できるビット数の範囲で扱える値を使っているので、どうしても誤差が発生してしまう事があるのです。この誤差を織り込み済みのものとしてなるべく広い範囲の小数を表現しようぜ！　としているのがコンピュータでよく使う浮動小数点数なのです。

浮動小数点数の対義語として使われるのが固定小数点数です。こちらは小数点の位置を固定する事で、整数の表現のようにビットを足していけば良い状態になっています。計算が早く、精度も高いので誤差があってはならない金融系のシステムなどで使われます。

ただし、小数点の位置を固定してしまうため、浮動小数点数に比べると表現できる値の範囲は小さくなります。

C#の浮動小数点数

C#で使っている浮動小数点数はfloatとdoubleの2種類があり、これらはIEEE 754に準拠しています。

……この1文で理解できたら多分このページを読む必要はないのですが、順番に説明していきます。

C#では浮動小数点数を扱うための型としてfloat(フロート)とdouble(ダブル)の2つが用意されています。マニアックな話をすると、floatやdoubleといった呼び方はエイリアス(あだ名とか通称)であって、実体はC#が動いている.NET Framework(ドットネット　フレームワーク)のSystem.Single型、System.Double型です。

floatが指しているのがSystem.Single型、doubleが指しているのがSystem.Double型になっています。C#側でエイリアスとなるキーワードを事前に定義してくれていることで、私たちユーザーはプログラムを書く時に楽をできるんです。ありがとうMicrosoftさん。

C#では「単精度浮動小数点数であるSystem.Single型 (= float)」と「倍精度浮動小数点数であるSystem.Double型 (= double)」が使われています。単精度なのでSingle、倍精度なのでDoubleと、.NET Framework側では割とそのまま名前が付けられています。

単精度浮動小数点数であるfloatは32ビット、倍精度浮動小数点数であるdoubleは64ビットで値を表現しています。使うビット数が単精度に比べて2倍なので倍精度という、よくよく見ればそのままな表現になっています。浮動小数点数、コワクナイヨ。

この仕組みはIEEE(Institute of Electrical and Electronic Engineers : 米国電気電子技術者協会)が技術標準として考えてくれていて、それに合わせる形でMicrosoft社で実装しています。754という数字は規格の通し番号のようなものです。

浮動小数点数の表し方

さて、沼に向かって一歩進んでみましょう。

浮動小数点は3つのパートから成り立っていて、符号、指数部、仮数部となっています。

\(Y=M \times B^{E}\)

ある浮動小数点数Yを表す際には上記の式で表します。Mは仮数部(Mantissa)、Bは基数(Base)、 Eは指数部(Exponent)です。

記号で書くとちょっとわかりにくいですが、以下のように実際に数字を使って表現すると分かりやすいです。

\(Y=1.234 \times 10^{3}\)

1.234が仮数部、10が基数、3が指数部ですね。浮動小数点数で表現している数値はこのような形式になっています。

コンピュータがデータを持つ際にはビットの並びで表現されます。以下の画像のサンプルとして並べたのは10進数の「16.75」のビット列です。

最上位ビットは仮数部の符号で0なら正、1なら負です。「16.75」は正の値なので以下の画像では符号のビットが0になっています。

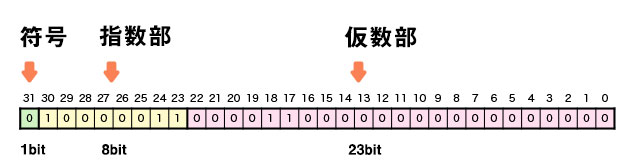
続いての8ビットは指数部になっていて、基数の何乗なのかを表しています。内部表現としては基数が2なので、2の何乗という形で表現されています。指数についても正負が存在するので、8ビットで表現できる-127から128までの範囲で値が表現されます。2の128乗は以下のように

\(2^{128} \approx 3.4 \times 10^{38}\)

となるため、floatで10進数を表現する場合は大体この値までとなっています。実際には指数部の値が128の場合や-127の場合は無限大やゼロなどの状態を表現しているため、通常の数値を表現する上で指数部のとりうる値は-126から127です。指数部が127を表しているときに仮数部のビットを全て1で埋めれば\(2^{128}\)に近い値になるので、「大体この値まで」と表現してみました。

残りの23ビットは仮数部です。こちらは桁を表すのではなく仮数を表すビットです。例えば上の図で表現している「16.75」を2進数で表記すると「10000.11」となります。仮数では小数点の位置を1.000011のように最上位ビットを1として正規化ことによって決め、そこに指数の値をかけることで小数を表現しています。

正規化というルールが決められているので、「1.」の部分はビットとしてデータを保持せず、暗黙的に存在するものとみなされます。なので、仮数部で表現するのは小数点以下の値となっています。

23ビットに暗黙の1ビットを加えて、合計24ビットを使って数値を表現できるので、\(2^{24}\)種類の数値を表現できるようになっています。これは10進数に直すと、

\(2^{24} = 16777216\)

となっており、常用対数を使って桁数を確認すると、

\(\log 2^{24} \approx 7.225\)

となるため、有効数字7桁まで表現できることになります。

UnityではTransformコンポーネントのPositionはそれぞれfloatになっており、極端に大きな値を入れると有効数字が足りなくて不思議な挙動をする事があります。非常に大きな数を扱っている場合には、例えば小さな数を足しても正規化した結果有効数字が足りなくなって反映されない事があります。こうした情報落ちも発生するので、Unityのマニュアルでは「あまり大きすぎる値を使用せず、スケールを変更して表現することを検討してください」といった注意書きがあったりします。

とまぁ浮動小数点数のコンピュータにおける表現を説明しましたが、値を表現するための箱が限られている点を認識してもらえればOKです。

綺麗に表現できない値

上の項目では「16.75」という綺麗に表現できる値を例に挙げました。しかし、浮動小数点数ではこのように綺麗に表現できる値の方が珍しいんです。

この記事の冒頭で例に挙げた「0.1」をビットで表現すると、以下のように循環小数になります。(計算方法は別ページでいつかまとめたいと思います)

0.00011001100110011..

「0011」の部分がずっと続いてしまう循環小数となっているため、floatやdoubleなどビット数が限られている範囲で表現するには、そのビット数の範囲で丸める必要があります。そのため、正確な値にならない事があるんですね。

例えば冒頭のソースコードのように、0.1を10回足し合わせて1.0にしたい場合、足し合わせる過程で微小な誤差が生まれて正確に1.0にならないんです。

試しに以下のように任意のクラスを作成し、0.1を10回足し合わせるメソッドを作成します。

CompareAddedValueToTarget()が0.1を足し合わせるメソッドになっています。ここでは値を直書きしていますが、引数で渡すようにしても良いと思います。

ビット列で違いを確認したかったので、引数の値からビット列を生成するShowBitArrayText()のメソッドを作っています。

このスクリプトを任意のGameObjectにアタッチしてゲームを実行すると以下のように出力されます。(コンソールの出力をコピペして整形しました)

0.1を10回足した値は正確に1にはならず、最下位ビットが1になっていました。その結果、10進法で表現すると「1.00000012」になっています。これに対して目標となる値の1.0は仮数部が全て0なので内部で認識している値は異なっており、比較の結果一致しませんでした。

比較するにはどうすべきか

floatの値は誤差がつきもの。そのため、単純に「==」や「Equals」で比較すると意図しない結果が生まれることもあります。

Microsoft社が提示している方法は2つあり、ひとつは許容できる桁数で丸め処理を行った後に比較を行う方法、もうひとつは微小な値を定義して、2つの値の差がこの微小な値より小さい場合に同じであると見なす方法です。

前者の許容できる桁数で丸め処理を行って比較する方法では、切り捨て、切り上げ、四捨五入、最近接偶数丸めなど、任意の丸め方法を使って丸め処理を行います。比較する両方の値で同じ桁数に揃えるので、微小な誤差による差異によって不一致と判断されることはなくなります。

後者の微小な値を定義する方法では、0よりほんの少しだけ大きな値を使います。高校数学で出てきた極限のε-δ論法に出てくる微小な値ε(イプシロン)にちなんで、変数名をepsilonにして比較を行う事が多いです。

Unityでは数学的な計算処理を行うクラスであるMathfクラスが用意されており、イプシロンもここで定義されています。さらにいうとイプシロンを使って比較を行ってくれるMathf.Approximately()というメソッドも用意されているので、floatの計算による誤差を考慮した上で比較を行う場合はMathf.Approximately()を使うと便利です。Approximatelyは「だいたい」とか「近似的に」という意味の言葉です。

試しに上で紹介したCompareAddedValueToTarget()のメソッドと同じように値を足し合わせ、比較にMathf.Approximately()を使ったメソッドを作成してみます。

ここでの出力は、比較した値が同じかそうでないかを表す文章です。

値の足し合わせ処理については変更を行いませんでしたが、Mathf.Approximately()を使うことによってTrueの場合の文章が出力されました。floatの計算による誤差が生まれたとしても、人間の意図に近い処理ができています。

なお、Mathf.Approximately()ではfloat型の値の比較を行うので、double型の値を比較する場合は自力で比較用のメソッドを用意する必要があります。イプシロンの値もfloatとdoubleで異なるので気をつけましょう。とはいっても難しいことはなくて、Microsoft社のSystem.Doubleのページにサンプルコードがあるのでこれを真似すればOKです。

docs.microsoft.com

Double 構造体 (System)

https://docs.microsoft.com/ja-jp/dotnet/api/system.double?view=netcore-3.1

倍精度浮動小数点数を表します。Represents a double-precision floating-point number.

まとめ

floatは有限のビット数で実数を表現するために、循環小数などではビット数の範囲に丸めることによる丸め誤差が生まれます。

誤差が生まれることによって等価比較において人間の意図しない結果が生まれる事があるので、誤差を考慮して比較を行う必要があります。

誤差を考慮した比較方法としてUnityではMathf.Approximately()という近似的に同じであると判断するメソッドがあるので、これを使うと便利です。