【Unity/C#】ヒープソートのためのヒープ作り入門

アルゴリズム、意識してますか？(挨拶)

今回はヒープソートをC#で実装！　……する前に、ヒープを表現する処理を実装します。

ヒープは子要素と親要素の値の関係に制限のある木構造のこと。

これ、知ってる人なら「うんうん」って言えるけど、最初は用語が多くて混乱しました。なのでなるべく簡単な言葉で説明できるように頑張ります(努力目標)

環境

macOS 10.14 Mojave

Unity2018.3.14f1

Unity Hub 2.1.0

アルゴリズムって？

アルゴリズムとは何かという話は別記事で書いたのでそちらをご覧くださいな。

エクスプラボ

アルゴリズムってなんやいね？　って時に読む記事【初心者向け】

https://ekulabo.com/whats-algorithm

初心者のうちからアルゴリズムを理解し、処理時間を意識していくと、超イケてるプログラミングが可能になります。慣れてる人は多分無意識のうちにやっていることなんですよね。

木構造って？

ここからが怒涛の解説ゾーン。

木構造(ツリー構造)は、データ構造(データの表現方法)の一種です。階層の上から下にたどってデータを取り出します。

データの繋がり方をみていくと目的のデータが探しやすいんです。

木構造ではひとつひとつの節(ノード)が枝(ブランチ)で繋がっています。最上位のノードは根(ルート)と呼ばれ、最下位のノードは葉(リーフ)と呼ばれます。下の図が木構造の例です。

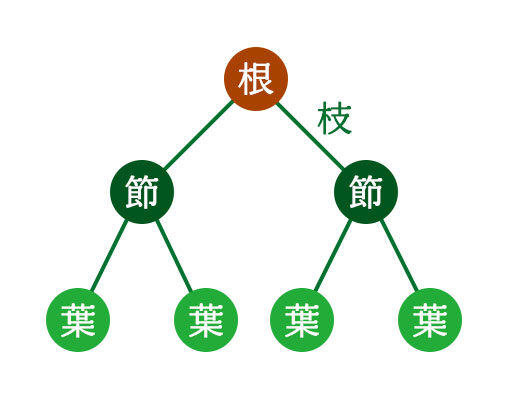
最初、この図を見ても意味分かんなかったんですよね。なんで根が上にあるのさ、と。普通の木ってこんな感じだもの。

ただ実際に木構造を書いてみると、最上位のノードが1つというのは見やすいんです。ピラミッドみたいで。

この根や節、葉にデータが入っているのが木構造なんです。

ヒープって？

ヒープ、あるいはヒープ木は、各節(ノード)で親子関係の大小が決まっている木構造のこと。この親子関係の大小は木全体で共通しています。

例えば各ノードで親要素の値が必ず子要素の値以上になる場合は、一番上の親要素である根が最大値となり、葉に向かっていくにつれ値が小さくなっていきます。

heapは名詞だと「積み重ねたもの」という意味で、大きなものの上にだんだんと小さいものを順番に積み上げていくイメージでしょうか。ジェンガのように大小大小大小小みたいな積み方はしないよーという熱い意思を感じます。

アルゴリズムの話でヒープと言った場合には二分ヒープ(バイナリヒープ)を指すことが多いです。ノードの子要素が最大でも2つとなる木構造です。

実はここまでの間にヒントがあったのですが、根が最大値、または最小値となるということは、ソート時に根の値を引っこ抜くことで順番にデータを格納できるということです。だからソートに使いやすいんですね。

データのくっつけ方にも特徴があって、同じ高さで埋まっていないノードがあったら、左から埋めていくんです。なるべく全てのノードが同じ高さに揃うようになっています。

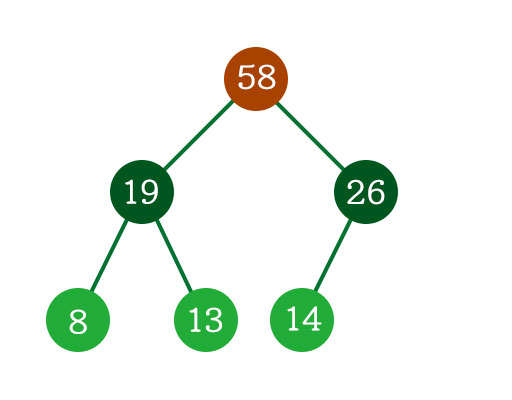
例えば以下のような二分ヒープがある場合、右の『26』の子要素がひとつになっています。新しく『25』を入れる場合、左の葉(『8』や『13』など)の下につけるのではなく、まだ埋まっていない『26』の下に追加します。

これが『25』の代わりに『1』を入れる場合でも同様です。親子関係の大小ルールからすると『8』の下に入れられそうですが、同じ高さで埋まっていないノードがあったらそこに左からつけていくルールによって『26』の下、『14』の右に入れることになります。

ルールをまとめると、

各節(ノード)で親子関係の大小が決まっている(木全体で大小は共通)

同じ高さで埋まっていないノードがあったらそこに左からつけていく(全て埋まったら次の高さへ)

となります。

このルールを徹底すると、ある規則が見えてきます。わかりやすく先ほどの図に番号を振ってみましょう。

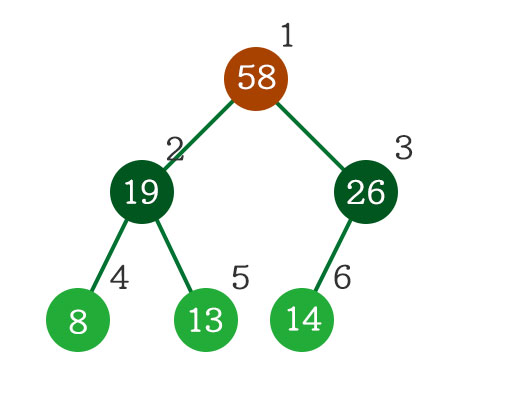
根の番号は\(2^0\)、その下のノードは左から\(2^1\)、\(2^1 + 1\)、さらにその下の葉は\(2^2\)、\(2^2 + 1\)、\(2^2 + 2\)といった形で表せます。2の乗数で表せるとか、まさにバイナリ。

他にも親の番号を2倍すれば左の子の番号になったり、子の番号を2で割って小数点以下を切り捨てれば親の番号になったりと、構造がわかりやすくなっています。

となると、ヒープの要素のそれぞれを番号で管理できるため、実は配列と相性が良いのです。

例えば上の画像であれば、{58, 19, 26, 8, 13, 14}とそのまま順番に入れていけばいいだけなので楽ちんです。C#の場合はインデックスが0から始まる点に注意が必要です。

ヒープソートに必要な処理

ヒープソートを行うにあたっては、配列がヒープのデータ構造になっている必要があります。

そこで、既存の配列をヒープ構造の配列として整理する処理を作成します。これはヒープへの追加処理を使うことで実現できます。ヒープへの追加処理は一般的にup-heapと呼ばれるそうなので、UpHeap()メソッドを作りましょうか。

また、ヒープ構造になった配列から最大値(根)を取り出して、ヒープを再構成する処理も作成する必要があります。こっちはヒープから根を削除する処理で、down-heapと呼ばれるそうです。名前はDownHeap()メソッドで決まりですね。

今回の記事ではヒープへの追加の機能を実装するところまでやります。

ヒープへの追加

ヒープへの追加アルゴリズムを画像で説明します。

いま、以下のように大きさが4の配列があり、インデックスの小さな方から5, 1, 8, 4の数値が格納されているとします。この配列について、根が最大値となるヒープ構造の配列に変換します。根が最大値ということは、各節(ノード)では親要素の値が子要素の値以上になるルールです。

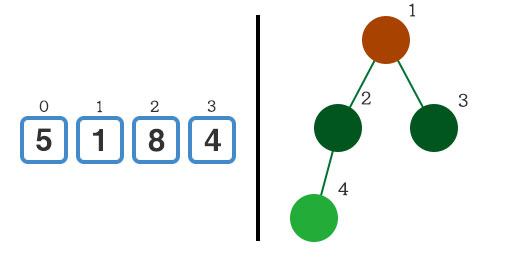
実は、配列を新しく作らなくてもこのままヒープ構造の配列に変換することができるのです。配列の左からヒープに追加していく「てい」で要素を並べ替えることでヒープを表現します。

ここではまずインデックス0の『5』からヒープに追加を行います。ヒープ構造の中では要素が1つだけなので、『5』は根になります。ヒープのインデックスと配列のインデックスが1ずれていることに注意してください。

続いてインデックス1の『1』をヒープに追加します。『5』と比較すると『1』の方が小さいので、『5』の子要素になります。

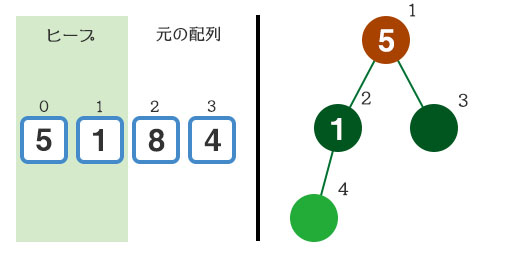
次はインデックス2の『8』をヒープに追加します。次に入る位置はヒープの3番なのですが、親要素である『5』と比較すると『8』の方が大きくなってしまいます。

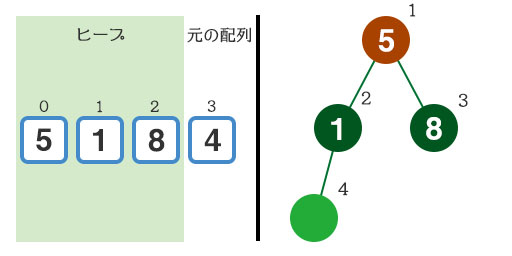
こうした場合は、ヒープの条件を満たすように、親要素と子要素を入れ替えます。『8』が親要素となることで、ヒープの条件が満たされました。ヒープの場合は現在確認中のインデックスから親要素のインデックスを求めることができるので、交換が簡単なんです。配列のインデックス+1が右の画像での番号なので、それを2で割って小数点以下を切り捨てれば親の番号になります。そこから1を引けば配列のインデックスに戻せます。

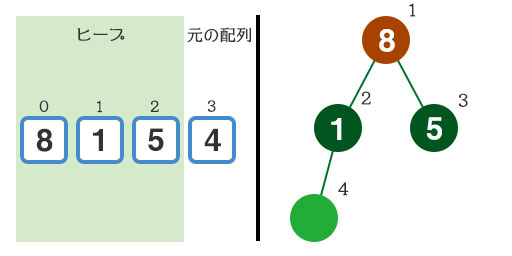
最後にインデックス3の『4』をヒープに追加します。『1』と『5』の高さは全て埋まったので、次は『1』の下から埋めていきますが、ここでも『1』と『4』はルールに合うように交換する必要があります。

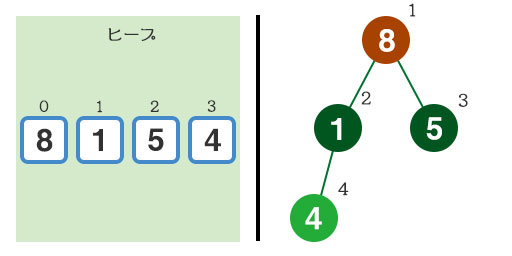
こちらも条件を満たすように入れ替えました。元々の配列要素を入れ替えるだけで、ヒープを表現している配列になりました。

ヒープへの追加を実装

これをC#で実装したコードがこちら。みっちりコメントを書いたので長くなってます。

今回作成したスクリプトは、ソートアルゴリズムで使っていた配列の中身を表示するためのメソッドを用意して継承しています。

SortBase.cs

こちらがヒープへの追加処理の本体です。

HeapSortPre.cs

ところどころコメントがヒープソートを意識していますが、今回はUpHeap()の処理です。

配列の数値は特に意味はありません。ランダムなら何でも大丈夫です。

外側のforループで配列の要素にアクセスしていき、ヒープへの追加を行います。交換が発生するかどうかは親要素との大小関係を確認しています。

もし交換が発生した場合は、さらなる交換が発生することを考えて確認中の要素のwhileループ内インデックス(currentIndex)を親要素のものにして、その親要素との比較を行っています。

whileループ内インデックス(currentIndex)が0、すなわち根の位置にくるか、交換が行われなかった場合は適切な位置に入ったと判断してwhileループを抜けます。

これを繰り返すことで、ヒープ構造の配列へと変換することができます。

このスクリプトをアタッチしてゲームを実行すると、コンソールに処理結果が出てきます。

実行結果

出力結果を整形すると以下のようになります。

ちゃんと並び変わっていますね。

一応ヒープの画像にして確認してみるとこうなります。

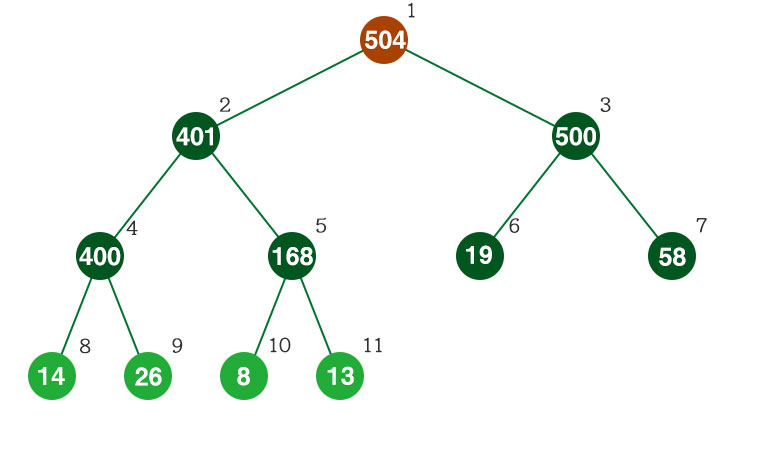
今回の配列だと値が離れているので顕著ですが、配列の前の方に大きな値が集まっているのが確認できます。

根が最大値になるため、各ノードでは親が大、子が小となっており、同じ高さでは左から埋まっています。ちゃんとヒープのルールも守られていますね。

まとめ

今回はヒープソートのアルゴリズムをC#で実装する準備として、配列をヒープ構造に変換するところまで扱いました。

法則さえ分かれば扱いやすいのがヒープの特徴です。初心者のうちはとっつきにくいかもしれませんが、絵と配列の対応をイメージできるようになると怖く無くなります。