【Unity/C#】コムソートのアルゴリズムを実装！(コムは櫛)
アルゴリズム、意識してますか？(挨拶)
アルゴリズムの例を考えるときにはまずソートから、という黄金律に従ってソートのアルゴリズムを片っ端からC#で実装していきます。
今回はコムソートのアルゴリズムをC#で実装します。コム(comb)は櫛を意味する英単語。コームと呼んだりする人もいます。
Unityを使うならArray.Sort()やList<T>.Sort()を……というツッコミが毎回入りそうでビクビクしているのですが、目的はアルゴリズムを体験することなので目を瞑っていただきとうございます。
環境
macOS 10.14 Mojave
Unity2018.3.14f1
Unity Hub 2.1.0
アルゴリズムって？
アルゴリズムとは何かという話は別記事で書いたのでそちらをご覧くださいな。
コムソートについて
コムソートはバブルソートの改良型で、適当な間隔を定義して、その要素同士で比較を行なっていきます。
例えば、まずは間隔5で要素を比較して、次に間隔4で比較して……といったように、最初に間隔を決めてから、徐々にその間隔を狭めていきます。
この間隔の決め方ですが、1.3で割って狭めていくとちょうど良いようです。元々の論文でも実験の結果から1.3が導き出されたみたい。この値を変えて実験してらっしゃる方がいたのでこちらも勉強になります。
なぜ比較する要素を離れたインデックス同士にしているかというと、例えば昇順に配列要素を並べ替えたい場合に、インデックスの大きな要素に小さい値が入っていると、それを前の方に持ってくるのに時間がかかってしまうためです。
バブルソートの場合は大きな値は1回のループで奥まで持っていけますが、逆に小さな値は1つしか動かせないので、それだけで1ループ必要になります。ループの中では値の比較が行われ続けているので、これはちょっと時間がかかります。
これを解消するため、コムソートでは離れた要素の比較・交換を行い、隣り合う要素の比較・交換の回数を減らせるようになっています。
最悪計算時間は\(O(n^2)\)ですが、実験的に平均計算時間が\(O(n\log n)\)となるため、バブルソートより高速にソートすることができます。
バブルソートについてはこちらの記事をご覧ください。
コムソートの仕組み
入れ替えの仕組みを簡単に説明します。
いま、以下のように大きさが8の配列があり、インデックスの小さな方から5, 1, 8, 4, 7, 2, 3, 6の数値が格納されているとします。この配列について、左から昇順で並べ替えることを考えます。
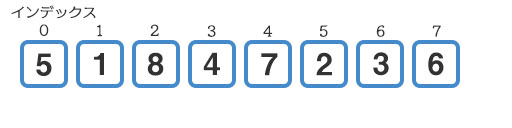
まずはじめに、要素の比較・交換を行う間隔(h)を決めます。配列の大きさは8なので、1.3で割って、小数点以下を切り捨てると6になります。この間隔6を使って、左端から確認していきます。
インデックス0の『5』から6離れた要素はインデックス6の『3』です。こちらを比較しましょう。
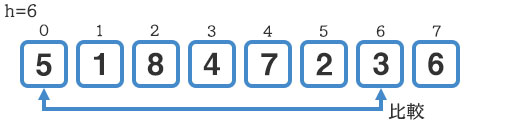
『3』の方が手前にいて欲しいので、『5』と交換します。
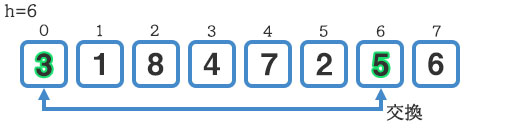
次にインデックスを増やして『1』と『6』を比較します。こちらは『1』の方が手前にいるのでそのままで大丈夫そうですね。
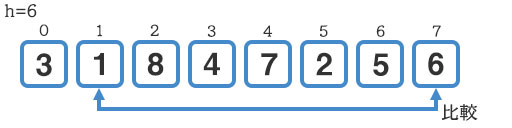
続いてインデックス2から6離れた要素……といきたいところですが、OutOfRange(範囲外)なので、このループは終了させなければなりません。
ループが終了したら、hの値を再計算します。hは6だったので、1.3で割って、小数点以下を切り捨てると4になります。次は間隔4で比較・交換を行なっていきます。
インデックス0の『3』とインデックス4の『7』を比較すると、どうやら並びは正しいようです。
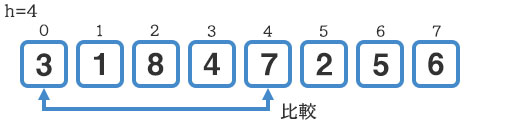
続いて『1』と『2』の比較です。こちらも交換は発生しません。
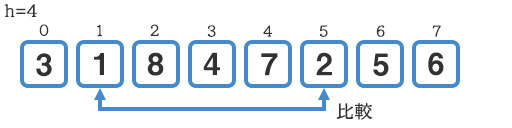
『8』と『5』の比較です。
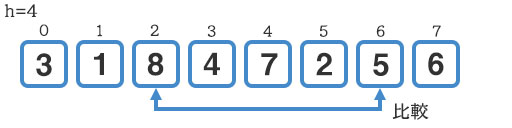
こちらは交換が発生し、『5』が前に送られます。
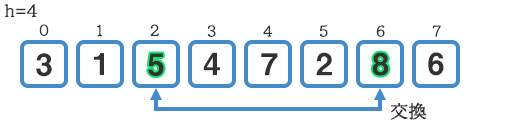
『4』と『6』の比較では交換は発生しません。これでこのループは終了です。
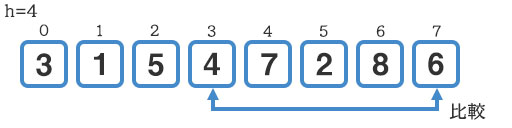
h=4だったので1.3で割って小数点以下を切り捨ててh=3で確認します。
このループでは『5』と『2』の交換、『7』と『6』の交換が発生します。
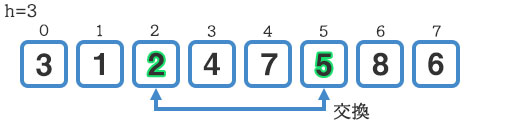
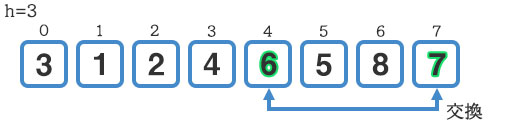
h=3だったので1.3で割って小数点以下を切り捨ててh=2で確認します。
このループでは『3』と『2』の交換が発生します。
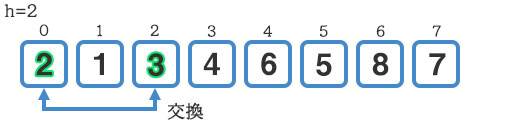
次はh=1になりますが、ここからはループ終了後に1.3で割らず、交換が発生しなくなるまでループを回します。隣り合う要素の比較・交換なので、ここからはバブルソートと同じですね。
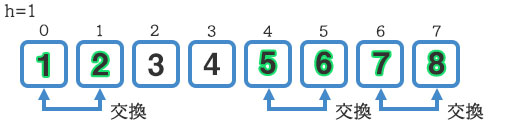
ループの中で交換が発生しなかったら処理終了です。
コムソートの実装
これをC#で実装したコードがこちら。みっちりコメントを書いたので長くなってます。
あと例のごとくWikipediaに書かれているCのコードを思いっきり参考にしてます。すみません。
今回作成したスクリプトは、配列の中身を表示するためのメソッドを用意して継承しています。
SortBase.cs
こちらがコムソートの本体です。
CombSort.cs
配列の数値は特に意味はありません。ランダムなら何でも大丈夫です。
バブルソートと同じように外側のループと内側のループが存在しています。こちらでは外側のループの実行回数が確定でないため、Whileループを使って処理が終了するまで回しています。
Whileループの開始時に間隔を表すhを計算しています。Mathf.FloorToIntは小数点以下切り捨ての処理です。
内側のforループの処理は単純で、要素同士の比較を行い、順番が違っていれば入れ替えを行います。範囲外の要素へのアクセスを防ぐため、終了条件にhを使っています。
このスクリプトをアタッチしてゲームを実行すると、コンソールに処理結果が出てきます。
実行結果
出力結果を整形すると以下のようになります。
並べ替えがちゃんとできていました。
バブルソートのように毎回値が確定するわけではないため、交換が発生しないことを確かめるループが入るのはやむなしです。
処理時間については要素を増やして他のソートとも比較してみたいですね。
まとめ
今回はコムソートのアルゴリズムをC#で実装しました。
平均計算時間が\(O(n\log n)\)となるだけあって、スムーズにソートされてる感じがします(主観)
実装が単純で速さを出せる点がメリットですね。
※追記
他の交換ソートのアルゴリズムと性能比較を行ったので、よかったらこちらもぜひ。思ったよりすごかったです。
ゲーム開発の攻略チャートを作りました！
「ゲームを作ってみたいけど、何から手を付けていいか分からない！」
そんなお悩みをお持ちの方向けに、todoがアプリをリリースした経験を中心に、ゲーム作りの手順や考慮すべき点をまとめたe-bookを作成しました。ゲーム作りはそれ自体がゲームのように楽しいプロセスなので、「攻略チャート」と名付けています。
ゲームを作り始めた時にぶつかる壁である「何をしたら良いのか分からない」という悩みを吹き飛ばしましょう！
-
前の記事
【Unity/C#】名前がかっこいい奇偶転置ソートのアルゴリズムを実装 2019.08.25
-
次の記事
【Unity/C#】精霊が並び替えるノームソートのアルゴリズムを実装！ 2019.08.27